Pythonで統計学入門―Pythonで相関係数を求めてみる―
以前の記事で、とある学年の国語の点数の偏差値を求めました。
今回は、「国語の点数が高い生徒は数学の点数も高い」ことが統計的に言うことができるかどうか、Python で計算します。
相関係数を Python で計算する
二つの値の間に関係性、つまり「ある値が高く(低く)なれば、もう一つの値も高く(低く)なる」と言う関係を統計学では、相関関係といい、どのくらい関係しているかを「相関係数」という値で表現します。
今回は以前の学年全員より人数を少なめにして、あるクラスの点数にしてみましょう
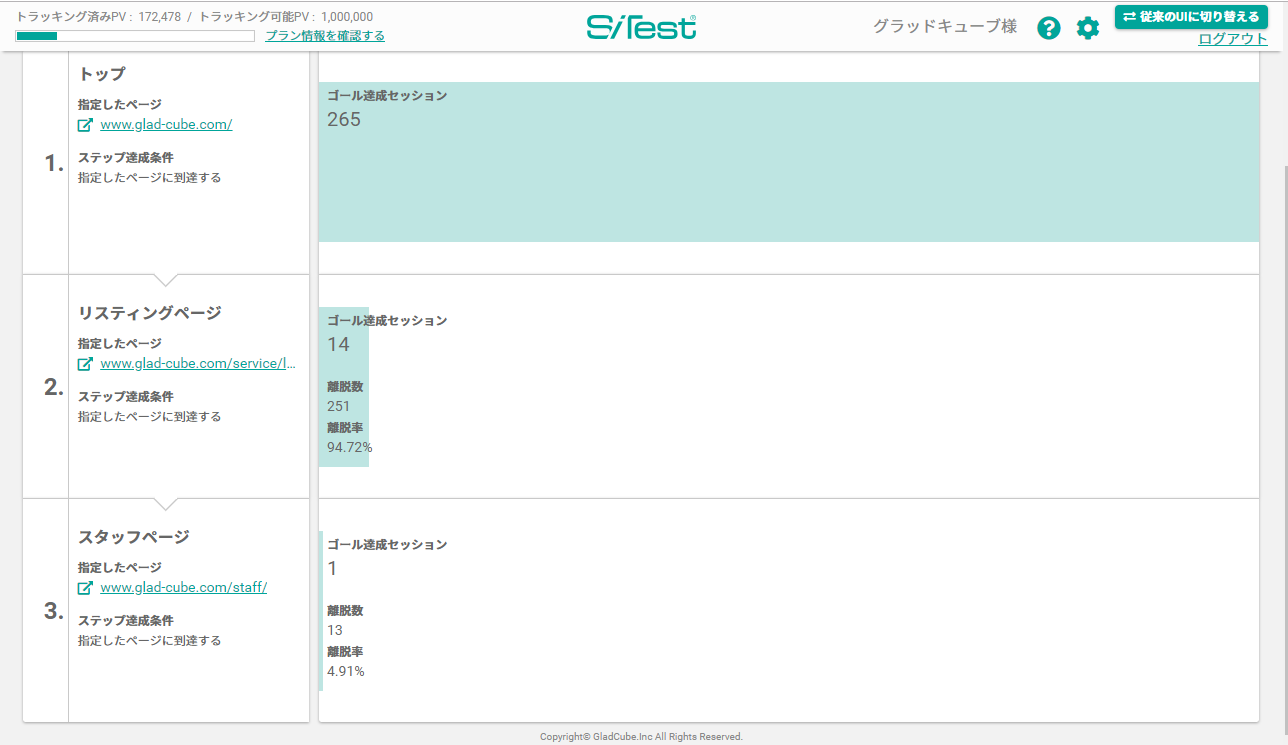
あるクラスの国語の点数、および数学の点数は以下のようになります。どのみち Python で計算するので、Python の配列で表現してしまいましょう。
japanese = [5, 73, 29, 63, 68, 28, 45, 78, 70, 93]
math = [11, 82, 25, 61, 66, 27, 42, 88, 71, 84]
さて、早速Pythonで計算します。モジュールである Numpy には、簡単に、相関係数を計算できる numpy.corrcoef 関数があるので、これを利用します。
import numpy
japanese = [5, 73, 29, 63, 68, 28, 45, 78, 70, 93]
math = [11, 82, 25, 61, 66, 27, 42, 88, 71, 84]
correlation = numpy.corrcoef(japanese, math)
print(correlation[0,1])
さて、すぐに結果が出ました。
0.975751057911
相関係数は-1〜+1の間の値をとり±1に近くほど、二つの値の間に関連が見られる。ということになります。
今回の値は0.975751057911となりましたので、この二つの点数の間にはかなり強い正の相関、すなわち国語の点数が高い生徒は、数学の点数も高い傾向にあるということが言えます。
相関関係は因果関係を証明するものではない
このように、二つの値の傾向を探るのに便利な相関係数ですが、ぜひ注意したい点があります。
それは「相関関係があるからといって、因果関係があることを証明できるわけではない」という点です。つまり、国語の点数が高い「から」数学の点数が高いというわけではないのです。
因果関係が成り立っているのなら、国語の勉強「だけ」をして国語の点数が高ければ、数学の勉強をしなくても、勝手に数学の点数も上がっていくことになります。そうでないことは、私たちの経験から見ても明らかです。
社会調査などでは相関関係を用いて、いろいろな主張がされていますが、それらが何を主張しているのか、注意してみる必要があります。相関関係があるのに過ぎないのに、まるで「××が低い(高い)から「○○が低い(高い)」という因果関係が存在しているかのような主張をしている例は、思ったよりもたくさんあります。
相関関係の限界をよく知り、面白い統計ライフを送ってください。それでは
-
お問い合わせ
SiTest の導入検討や
他社ツールとの違い・比較について
弊社のプロフェッショナルが
喜んでサポートいたします。 -
コンサルティング
ヒートマップの活用、ABテストの実施や
フォームの改善でお困りの方は、
弊社のプロフェッショナルが
コンサルティングいたします。
今すぐお気軽にご相談ください。
今すぐお気軽に
ご相談ください。
(平日 10:00~19:00)
今すぐお気軽に
ご相談ください。
0120-90-5794
(平日 10:00~19:00)
グラッドキューブは
「ISMS認証」を取得しています。

認証範囲:
インターネットマーケティング支援事業、インターネットASPサービスの提供、コンテンツメディア事業
「ISMS認証」とは、財団法人・日本情報処理開発協会が定めた企業の情報情報セキュリティマネジメントシステムの評価制度です。