機械学習に必須の数学的知識をおさらいしよう ｜ SiTest (サイテスト) ブログ

機械学習の基礎を学ぼうとして本を手に取った時数式の羅列で読む気をなくした経験はありませんか？
本記事では機械学習を学ぶ上でよく出会うであろう線形代数とその他の数学的知識についてまとめてみました。

あまり耳慣れない言葉ですが、大学数学を学んだ方は馴染みがあるのではないでしょうか。
線形代数です。
高校2年で習うベクトルや、行列を扱う学問です。

さらにそれらの延長としてテンソル(Tensor)というものがあります。(テンソルの中にベクトルやスカラがあります。)
TensorFlowはこのテンソルを用いて機械学習を実装するライブラリです。

テンソルには階層が存在し各階で呼び方や性質が異なります。

0階をスカラと呼び大きさを示します。
重さ、長さ等があたります。

1階をベクトルと呼び大きさと向きを示します。

2階を行列と呼びます。
行列は、m✕n型の行列と表現し数値が縦にm個横にn個並んだものです。

主な性質として

・足し算はm✕n型同士で行える。同じ位置の値を足し合わせればいいです。

 

・スカラ✕行列の場合は各位置の値がスカラ倍になります。

 

・行列✕行列の掛け算は少し複雑で次の様になります。

 

・違う型の行列を掛けた時はどうなりますでしょうか？

 

・積は可換ではない。掛ける順番を変更すると結果が変わります。

 

・行列の積は結合法則が成立する。

 

・分配法則が成立する

 

TensorFlowのチュートリアルにあるMNISTはこの行列の性質を理解していれば理解できます。
主な特徴として

また3階以上のテンソルは高階テンソルと呼び数学的には表記しにくいのですが、m✕n型の行列が更にk個ある状態です。
4階になるとさらに3階のテンソルがl個と言った具合に増えていきます。

プログラミングの世界では配列を入れ子にしていくことで表現ができるので表現はし易いです。
さらに大体のプログラム言語にあるfor文等で繰り返し実行することで中身を操作することも可能となります。

少し突っ込んだ本等を読んでいると微分の話しもでてきます。

恐らく知らない人はいないと思いますが、特定の変数に注目した時その変数がどのように変化するのかを求める演算です。

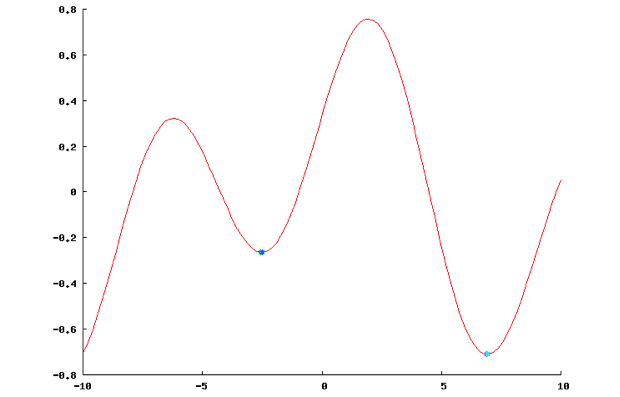
機械学習においては勾配降下法と言い連続する複数の極小値をもつグラフに数値を代入して最小値を求めていきます。
ただしグラフの極小値の溝にハマってしまうと正しく最小値が求められないことがあるので一度に移動する値を調整する必要があります。

最後に統計です。
統計とは既にデータが存在する時その傾向をつかむための学問です。
統計学と機械学習は別物ではありますが、機械学習にも統計の要素は入ってきます。

統計学と機械学習の違いとして、
統計学はデータからどういう状態なのかを説明する為の学問で、機械学習はデータから予測する為の機能です。

いかがでしたでしょうか？
主に行列の性質の話しが主になってしまいましたが、機械学習を理解する上で非常に重要な項目となっています。
機械学習の本を読む際これらの数学的知識を理解しておけば本をより楽に理解することができるでしょう。