A/B テスト結果を正しく判断するために～②t検定とは？ ｜ SiTest (サイテスト) ブログ

A/Bテストを行った際に、その結果を分析・判断するには「仮説検定」という方法を用いることを前回お話しいたしました（参考：A/B テスト結果を正しく判断するために～①仮説検定について）。検定には様々な種類があり、状況により使い分けを行うのが本来であれば正しいのです。
今回は、様々な検定手法の中から、t検定をご紹介します。

究極を言えば、無限大に近いサンプル数があれば、成果が良い方を「勝ち」にして、そちらのパターンのほうが成果が上がるものなのだ、と結論付けることができます。
しかし、大量のサンプルを集めるほどの時間もないし、費用もないし、そもそもそこまで訪問数が多くないという方も多いかと思います。そこで、そこまで多くないサンプル数でも、今の結果が「偶然の産物」ではなく、この先ずっと今の結果の傾向が続くよ、とロジックを持って証明できれば、それをもってテストの結果として見よう、というのが「仮説検定」を用いた判断です。
「偶然の産物」かどうかを確かめるために用いるのが「有意差」という考え方です。有意差があるかどうかを確かめるのが「仮説検定」ということになります。

WikiPediaには、以下のように書かれています。

t検定（ティーけんてい）とは、帰無仮説が正しいと仮定した場合に、統計量がt分布に従うことを利用する統計学的検定法の総称である。
母集団が正規分布に従うと仮定するパラメトリック検定法であり、t分布が直接、もとの平均や標準偏差にはよらない（ただし自由度による）ことを利用している。
２組の標本について平均に有意差があるかどうかの検定などに用いられる。統計的仮説検定の一つ。
日本工業規格では、「検定統計量が、帰無仮説の下でt分布に従うことを仮定して行う統計的検定。」と定義している。

正規分布に従うと仮定されたデータに対して仮説検定を行うためには、帰無仮説のもとで正規化という作業が必要です。標準化には「母分散」という指標を用います。
しかし、「母分散」が未知の場合には、この作業を行うことができません。そこで、その代わりに標本分散による推定値である「標本不偏分散」を用います。この場合、標準正規分布ではなくt分布に従います。
標準化によって得られた値をt値、t値とt分布表から求められる値をp値と言います。p値があらかじめ決めておいた有意水準よりも小さい場合、帰無仮説を棄却します。これは前回ご説明したとおりです。

t検定は、大きく３つの種類に分けられます。

※そもそも、正規分布とは？

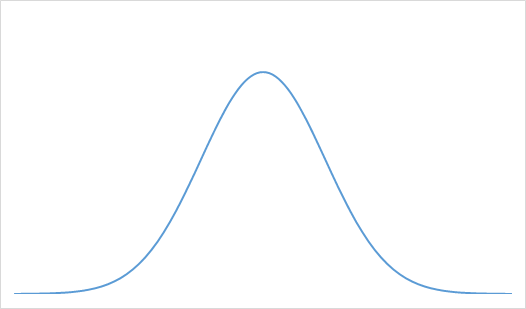
正規分布（normal distribution）

統計学を理解する上で、最も大切でスタンダードな確率分布と言ってもよいものです。自然界の様々な現象によく当てはまることから、「ありふれた（=normal）」が当てられています。上記掲載のグラフのように、左右対称の曲線となります。
基本的な性質としては、以下のようなことが挙げられます。

• ・平均値、最頻値、中央値が一致する。
• ・上記値を中心に左右対称である。（直線x=μに関して対称）
• ・x軸が漸近線である。
• ・分散（もしくは標準偏差）が大きくなると、曲線の山は低くなり平らに近くなる。
• ・分散（もしくは標準偏差）が小さくなると、曲線の山は高くなり尖った形になる。

詳細な式など、学びたい場合には、こちらのサイトを参考にされて下さい。
（正規分布のわかりやすいまとめ）

１．正規分布に従う１つの母集団の、母平均が特定の値と等しいかの検定（１標本問題）

サンプルサイズnの標本データ、x1, x2, …, xn が独立に同じ正規分布N（μ,σ^2）に従うと仮定します。
ここで、
・帰無仮説H0：μ=μ0
・対立仮説H1：μ≠μ0
という仮説検定を考えてみます。

母分散は未知ですから、σ^2も未知。このとき、σ^2の推定値として不偏分散を用いて標準化を行います。

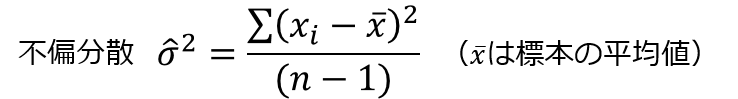
帰無仮説のもとで得られるt値は、

（tは自由度n-1のt分布に従う）
このt値と自由度、t分布表を用いて、p値（第一種の過誤の確率）を求め、予め定めた有意水準に満たなければ、帰無仮説を棄却します。

２．正規分布に従う２つの母集団の、母平均の差に関する検定（２標本問題）

サンプルサイズm, nの２つの標本データ、x1, x2, …,xm と y1, y2, …,yn がそれぞれ正規分布N（μ1,σ1^2）、N（μ2,σ2^2）に従うと仮定します。
この時、２標本の母平均の差δ に関する仮説検定
・帰無仮説H0：δ=0
・対立仮説H1：δ≠0
について考えてみます。（２つの母集団の平均値の差が0であることを帰無仮説とする）
ここで、２つの標本の平均値の差も正規分布に従う、ということを利用します。

①２つの標本の母分散が等しい、と仮定した上で行う検定

母分散が等しいと仮定すると、σ1=σ2 ですので、σ1^2=σ2^2=σ^2とすることができます。加重平均を用いて推定量を計算します。

帰無仮説のもと、

これが、t検定に用いられるt値です。（tは自由度m+n-2のt分布に従う）
t分布表で求めたp値が有意水準以下であれば、2つの母集団の平均に有意差が認められるといえます。

②２つの標本の等分散性を仮定できないときに行う検定

２つの標本の母分散が等しいと仮定できない場合には、こちらの検定（Welchのt検定）を使用します。
統計学では、検定を繰り返し行うと「多重性の問題（第一種の過誤の確率が大きくなる問題）」が生じます。そのため、２標本のt検定を行う場合には、①でご紹介した等分散性の検定を行わず、等分散かどうかを考慮する必要がないこちらの検定を行ったほうが良いと、いう考えが一般的です。

これにより、t値、p値を求めます。
自由度fは、下記の通りの式となります。（fは整数とはならない場合があります）

t分布表で求めたp値が有意水準以下であれば、2つの母集団の平均に有意差が認められるといえます。

③２つの標本において、標本の１つ１つに何らかの関係が認められるときに行う検定

この検定は、よく薬の処方の前後での血圧の値や血糖値の値などが例題に上がります。患者さんに対して降圧剤を処方した際、それぞれの患者さんの、薬を処方する前の血圧をx1, x2, …, xn、処方された薬を服用後の血圧をy1, y2, …, yn とします。このように２標本の各データが１対１対応のデータのときには、こういった対応を考慮に入れて、対を作って検定するほうが望ましいです。

帰無仮説H0：薬の処方前と処方後で母平均は等しい（μd=μ0）
対立仮説H1：薬の処方前と処方後で母平均が異なる（μd≠μ0）
この帰無仮説のもとで、dを標準化すると、

（tは自由度n-1のt分布に従う）
このt値と自由度、t分布表を用いて、p値（第一種の過誤の確率）を求め、予め定めた有意水準に満たなければ、帰無仮説を棄却します。

３．回帰分析における回帰係数が０であるかの検定

単回帰分析では、一つの目的変数を、一つの説明変数で予測することを考えます。具体的には、y=a+bx という回帰直線モデルでデータを代表させます。この回帰直線の切片 a と、傾き b は最小二乗法によって求めることができます。切片と傾きは、t検定により、ゼロではないかどうかの検定ができます。

このt値と自由度、t分布表を用いて、p値（第一種の過誤の確率）を求め、予め定めた有意水準に満たなければ、帰無仮説を棄却します。

今回は、最もよく使用され、基本となるt検定について、ざっとまとめてお伝えいたしました。こちらの考え方、検定のしかたをよく頭に入れておくことで他の検定も理解しやすくなりますので、難しい式も出てきましたが、一度じっくりと学んでいただけますと幸いです。
次回は、また他の検定方法をご紹介します。

弊社では、こうした検定の仕組みを理解した上で組み込み、ABテストの結果の検証に利用しています。ABテストを行いたい方、どこで終えればよいかなど、コンサルテーションも行っておりますので、ぜひお気軽にお問い合わせください。
SiTest トライアルの申込みはこちら
サイト改善サポートサービス詳細はこちら