機械学習の理解に必須!ベイズ統計学の基礎の基礎
昨今の人工知能ブームで、人工知能がまるで万能かのような話があちらこちらで聞こえてくるようになりました。
しかし、人工知能を紐解いていくと、そんな夢みたいな話はありません。
結局のところ、線形代数、確率統計などの集合体であって、その理解なしに本質はわからないものです。
今回は、機械学習の理解に必須のベイズ統計にスポットを当てたいと思います。
参考:上司から「AIで何とかしろ」といわれたら(日経College Cafe)
少し数学的知識が必要になってくるため、まずは簡単に概要を知りたいという方は、
ランプの魔人「Akinator」でも使われている!ベイズ定理とは?
ベイズ推定とは?モンティ・ホール問題を解いてみよう!からどうぞ。
[Index]
1.まずはベイズの定理をなんとなく知った気になろう
– 条件付き確率について
– ベイズの定理とは?
2.ベイズ統計学について
– 客観確率についてざっとおさらい
– 分割
– 乗法定理・加法定理
– 周辺化
– ベージの定理(再掲)
※検診問題
– 逆確率
– 独立
– 客観確率と主観確率
– 客観確率
– 主観確率
※モンティ・ホール問題
3.ベイズの定理の使用法
※血液鑑定問題
4.ベイズ更新
最後に
1.まずはベイズの定理をなんとなく知った気になろう
条件付き確率について
高校数学で出てくる条件付き確率。言葉の通り、「とある条件下での確率」です。
例題で言うとこんな感じです。
3本の当たりくじと、7本のハズレくじが入っている箱があります。
A君がくじを引いたあと、B君がくじを引きました。
このとき、A君が当たりくじを引いた時、B君が当たりくじを引く確率を求めなさい
「A君がはずれくじを引いた」という条件下で、B君が当たりくじを引く確率を求めます。
A君がくじを引かずにB君がくじを引いた時、当たりくじを引く確率は 3/10 です。
A君があたりを引いてしまえば、なんとなくその後に引くB君は不利な気がしますね。
まさにこれが、「条件付き確率」です。本当に不利なのか調べてみましょう。
A君が当たりくじを引く確率をP(A)
B君が当たりくじを引く確率をP(B)
と置き整理すると、このような表が書けますね。

もしも、前提条件が同じ(A君とB君が同時にくじを引く場合など)ですと、
A君もB君も当たりである確率は、P(A∩B)で表すことができます。
しかし、今回は前提条件が「A君が当たりを引いた場合」ですから、
表の色がついている部分だけを考えなさい、という問題に変わっているわけですね。
A君が当たりくじを引いたあと、B君が当たりくじを引く確率をP(B│A)
と書きます。
すると、以下の公式が成り立ちます。
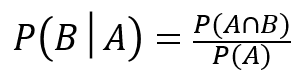
確率は、(とある事象が起こる場合の数)/(全体の場合の数)ですから、
今回は「全体の場合の数」がP(A)になるんですね。
では、実際に確率を求めてみましょう。
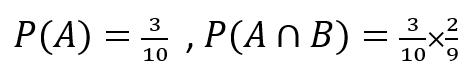
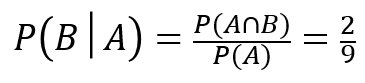
3/10 と 2/9 を比べてみると、
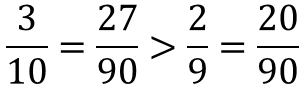
となり、
やはり、B君は不利になりましたね。。。
このように、とある条件下での確率を考えることがベイズの定理の第1歩です。
ベイズの定理とは?
先程、こんな公式が出てきましたね。
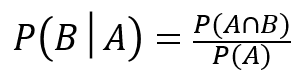
これをちょっと変形すると、

こうなります。
これは、下記表の色をついた部分で考えたときに導けるのでしたね。

同じように、今度はBに着目して、この色がついた部分で考えてみましょう。

すると、以下のように立式することができます。
先程のAとBを入れ替えて考えれば良いだけです。
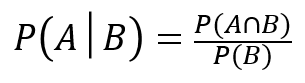
これを少し変形すると、
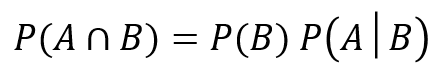
こうなります。
導き出した2つの式を合体させましょう!!
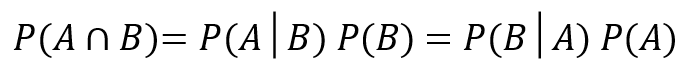
これが、ベイズの定理の式です。
ベイズ統計の基本となる考え方ですので、まずはここまで押さえておきましょう。
2.ベイズ統計学について
さて、ではベイズ統計学(Bayesian Statistics)とはどういうものなのでしょうか?
ベイズ統計学は、1章でご紹介したベイズの定理にもとづき展開される統計学の体系の1つです。
これに対し、現在みなさんがよく知っている伝統的な統計学の体系は「ネイマン・ピアソン理論」と呼ばれ、検定・推定などといった手法は幅広く知られ親しまれています。
(以前、「ABテストの終わりを見極める!統計的有意差と仮説検定入門」でお伝えした手法は、まさにこちらの手法です)
ベイズ統計学では「主観確率」というものを用いるため、伝統的な統計学で用いられている「客観確率」に慣れていると少し戸惑いますが、
伝統的統計学では無理矢理に不自然な仮定をせねばならなかったことが、全て確率の演算で一貫して行えるという点で、広く柔軟な適用が可能になります。
どちらも良い点と悪い点がありますので、どちらかの信奉者になるのではなく、使い分けができるとなお良しです。
客観確率についてざっとおさらい
まずは「客観確率」から見ていくことにします。ベイズ統計学に踏み込む前に、まず基本を押さえておきましょう。
その前に、確率を語るにおいて基本となる用語を定義しておきましょう。
さて、事象の数を数える関数Nを、
N(A)=「事象Aに含まれる根元事象の数」と定義すると、確率は
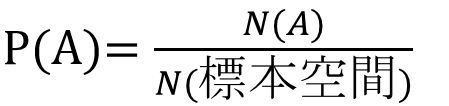
と表すことができます。
[Example]
赤玉30個、青玉70個、全部で100個の玉があります。
玉を1つ取り出すときに、その玉が赤玉である確率Pは?
この場合、
「100個の玉から1個取り出す」という試行について考え、
「取り出した玉が赤玉だった」という事象Aについての考察を行う。
「標本空間の玉の数N(標本空間)」 = 100,
「取り出した玉が赤玉」という事象の数N(A) = 30,
よって、P(A) = 30/100 = 3/10
となります。
ここで、必要な確率の知識を総ざらえしておきましょう。
分割
a組の事象
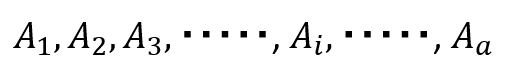
が、互いに共通の根元事象を含まず、同時に標本空間を表現しているとする。
標本空間がaコに分割されている場合、その確率の総和は必ず1になる。
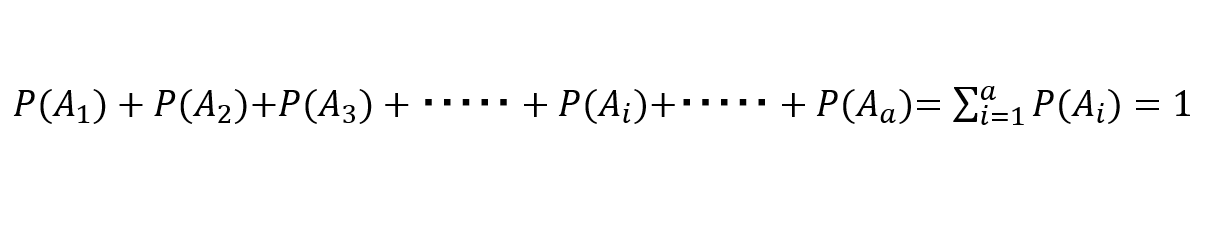
何のことやら、と思われるかもしれませんが、確率を数式として取り扱う際に必須の「確率密度関数」という考え方です。
通常、機械学習の話の中で登場する「◯◯確率」というのは、この密度関数を指すと考えて良いです。
乗法定理・加法定理
・乗法定理
2つの確率変数のA、Bの同時分布に関して、以下の式が成り立ちます。
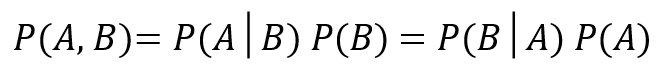
先ほど、重要な式ですよと言って提示させていただいた式と同じです。
AとBの片方の確率変数が決まり、その条件下でもう片方の確率変数が決まることと、AとBの確率変数が同時に決まることは同じだということです。
たくさんある玉の中から、一個を引いてからもう一個引くことと、二個同時に引くことは確率的には同じことであるということです。
感覚的に、理解できる内容ではないでしょうか。
・加法定理
もう一つの式がこちら。
上記でも出てきた同時確率について、こんな式が成り立つのです。

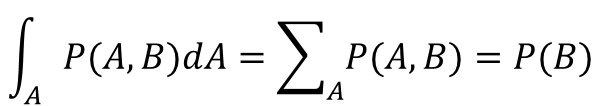
AとBの同時確率で、Aについてのすべての場合を足し合わせると、Bの確率になる。
同時確率についてどんな条件がついていようと、その条件を全て足し合わせると、条件がないのと同じになります。
周辺化
乗法定理と加法定理がなんとなく理解できたら、あとはこれらを基に式変形してやると求めることができます。
加法定理を逆向きに使って、乗法定理を代入しただけです。
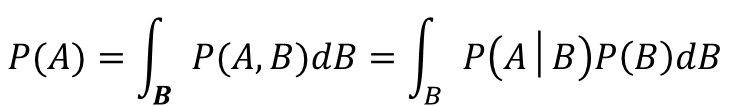
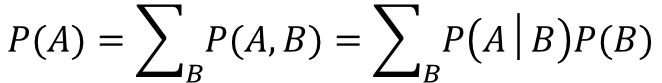
P(A)をいきなり求めようと思うと難しい局面でも、Bというデータを介在したAの情報があれば、周辺化をすれば計算できるという場面も出てくると思います。
さて、ここまでの内容を総ざらえしながら、ベイズの定理を見ていきましょう。
ベイズの定理(再掲)

「事前確率」をP(A)とすると、事象Bが起こった際の確率P(A│B)を「事後確率」と言います。
とある病気Aは、1万人あたり60人の割合で罹患していることが知られています。
病気Aに罹患している人が検診Bを受けると、7割の確率で陽性になります。
健常な人が検診Bを受けると、9割の確率で陰性になります。
検診Bにより陽性と判定されたとき、その人が病気Aに罹患している確率は?
P(A│B):Bが起こった際のAの確率、を求める問題です。
まずは、表を書いて整理してみましょう。
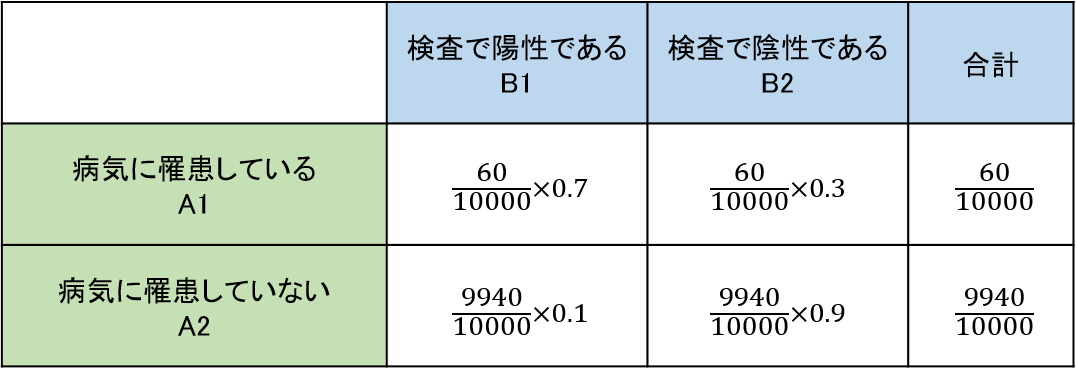
求めるのは、P(A1│B1):検査で陽性だった(B1)ときに、実際に罹患している(A1)確率、ということになります。
ベイズの定理より、
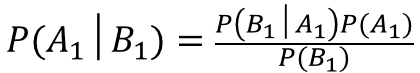
ここで、分母P(B1)について、周辺化を用いると、
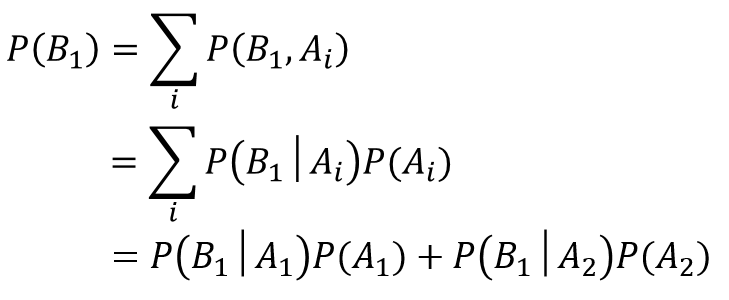
ですので、元の式に代入すると、以下の通りになります。
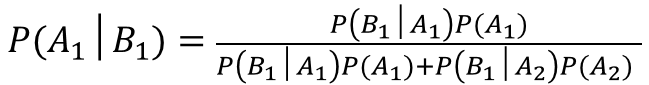
P(A1):病気に罹患している事前確率
P(A2):病気に罹患していない事前確率
P(B1│A1):病気に罹患している人が陽性である確率
P(B1│A2):病気に罹患していない人が陽性になる確率
あとは、それぞれの場所に値を代入していきましょう。
P(B1│A1)P(A1)=P(A1∩B1)=(60/10000)×0.7
P(B1│A2)P(A2)=P(A2∩B1)=(9940/10000)×0.1 ですから、
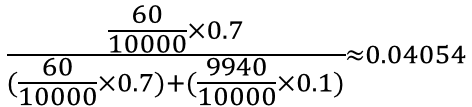
つまり、検査Bで陽性だったときに実際に病気Aに罹患している確率は、約4.05% ということになります。
おそらく、普段の我々の感覚からするとびっくりするような低い値だと思います。この感覚のズレこそが、確率統計を勉強する一つの意義でもあります。
逆確率
通常の条件付き確率は、時間の流れに沿って「Aが起こったときの結果Bの確率」を求めますから、P(B│A) = P(結果│原因) を求めるわけです。
しかし、ベイズの定理では、時間の流れに逆らって「結果BだったときのAの確率」を求めます。P(A│B) = P(原因│結果)を求めます。
さて、上記の検診問題では、
ですよね。
このような、原因の確率のことを、「逆確率」と呼びます。
独立
もう一つ、重要な確率の性質に「独立」かどうか、というものがあります。
試行Aと試行Bが互いに影響を受けない状態を独立といいます。
最も簡単な例がサイコロです。
サイコロAとサイコロBを投げた時、Aの出目の結果とBの出目の結果は影響しませんよね。
この時、AとBは互いに独立であるといいます。
式で書くと、こんな感じになります。
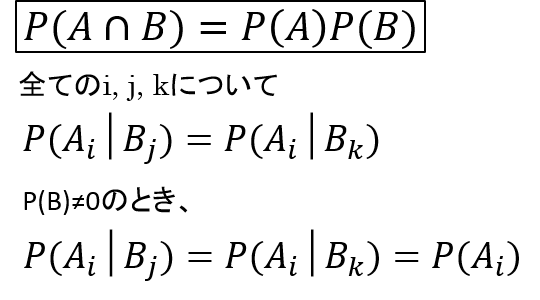
そして、AとBが互いに独立である場合には、AとBの同時確率は個々の確率の積で表すことができます。
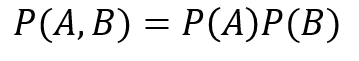
客観確率と主観確率
イギリスの統計学者で現代の推計統計学の確立者でもあるロナルド・フィッシャーは、ベイズ統計学を「完全に葬り去らなければならない」と強く批判したと伝えられています。その言葉の鍵となるのが、「客観確率」「主観確率」という考え方です。
先程まで様々な事象で見てきた確率は、全て「データに基づいて」計算されています。ですから、ベイズ統計学の全てを否定しているわけではありません。しかしながら、(特に逆確率を求める際)観測上の根拠が前もって存在しない(=データがない)状態で、既知の標本が取り出された母集団に関する推論を確率的に表現するのは間違っている!と主張しているのです。
客観確率
世界中に存在する頻度や傾向性など、我々の主観とは独立に存在するものとしての確率。実験や思考実験によって求められ、客観的な観測結果と比較できるランダムな事象についての確率。
ある事象が起きる頻度の観測結果を基に、無限回繰り返した際に収束する極限値として定義されるのが一般的で、頻度主義とも言われます。
主観確率
個々の人間が考える主観的な信念、信頼度のこと。なので、客観的に求めることはできません。
・・・では、こんな不確実な確率をなぜ使用するのでしょうか。そこには、客観確率の限界があります。
頻度主義を取った場合、一回限りの事象について確率を割り振ることができない。
(例)
「サイコロAを振って1が出る確率」は頻度主義で「サイコロAを無限回振ったときに1が出る確率」と置き換えられる。では、「サイコロAを一度振って、もう一度サイコロAを振ったときに1が出る確率」はどう表現すればよいのか?
また、頻度では表せない問題のときも、表現に困る。
(例)
ある事件の捜査線上に容疑者Aが浮上した。この容疑者Aが犯人であるかどうか?
とはいえ、主観的な信念、信頼度を重視すると正確な判断ができませんよ、という有名な例を一つ。
目の前に3枚の閉まったドアA, B, Cがある。1つのドアの後ろには景品の新車が、残りの2つのドアの後ろにはハズレを意味するヤギがいる。あなたが1つのドアを選択した後、司会者のモンティは残りのドアの内ヤギがいる方のドアを開けて見せてくれる。そして最初に選んだドアを、残っているドアに変更しても良いと告げられる。さて、あなたはドアを変更すべきか?
ここで重要なのは、モンティがドアを必ず開け、そのドアは必ずハズレのドアであることです(これでベイズの定理での事後確率が有効となる)。
通常の感覚では、初めに選んだ扉が当たりの確率は1/3。その後、扉を開けてくれたことで選択肢は2つになり、そのどちらかが当たりなので確率は1/2に上昇。選択を変えても変えなくても確率は1/2ずつだから、変えようが変えまいが結果は変わらない・・そう思うでしょう。では、実際に計算してみましょう。
はじめに選んだドアをA、残りのドアをB、Cとします。
その際に、それぞれのドアの後ろに景品の新車がある確率と、司会のモンティがそれぞれのドアを開ける確率を表にしてみると次のようになる。
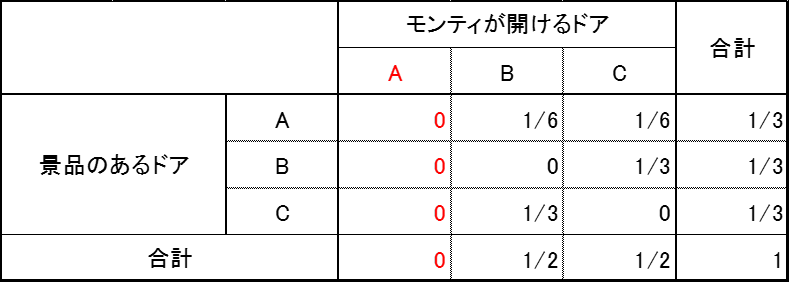
(各確率は次のように求めます)
①ドアAが当たり、はずれのドアのうちBを開ける確率 (1/3)×(1/2) = 1/6
②ドアAが当たり、はずれのドアのうちCを開ける確率 (1/3)×(1/2) = 1/6
③ドアBが当たり、Aはもともと選択されていて開けられないからはずれのCを選ぶしかない、1/3
④ドアCが当たり、Aはもともと選択されていて開けられないからはずれのBを選ぶしかない、1/3
ドアAをはじめに選んでいて、そのままでいるとすると、上記①と②のときのみ当たりだから 1/3
ドアAをはじめに選んでいて、そのあと選択を変更したとすると、上記の③④のときに当たりだから 1/3+1/3 = 2/3
よって、選択を変えたほうが、選択を変えないよりも2倍の確率で当たりやすくなる。だから選択を変えたほうが良い。
このように、自らの主観で物事を考えると実際の確率とは異なることがあることがわかります。
3.ベイズの定理の使用法
前述の通り、事前確率、条件付き確率ともに客観確率の場合は何の問題もなくベイズの定理を使用ができました。どちらかに主観確率が出てきた場合、その主観確率が間違っている可能性があるから注意して使用しなければいけないことも学びました。では、主観確率が間違っている可能性を出来る限り排除するにはどうすればよいのでしょうか。
とある都市で殺人事件が発生した。現場に残された犯人の血液を鑑定したところ、この都市に住むA氏と血液の特徴が一致したという。この血液の特徴は特殊な方法の鑑定であり、100,000回の鑑定で誤りは1回と、格段の精度を誇っている。しかし、これ以外には何の証拠もない。この時、A氏を犯人として検挙してしまって大丈夫だろうか。
A氏が犯人である確率を探っていきましょう。
血液鑑定で一致し、犯人である確率をP(犯人│一致)と書くことにすると、ベイズの定理から以下の通りの式が導ける。
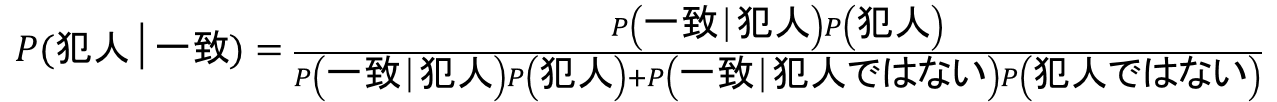
A氏が犯人であれば、現場に残された血液もA氏のものであるから、
P(一致│犯人) = 1
犯人でないにも関わらず、血液鑑定が一致してしまう確率は、
P(一致│犯人ではない) = 1/100000
また、
P(犯人ではない) = 1-P(犯人)
よって、このように変形ができます。
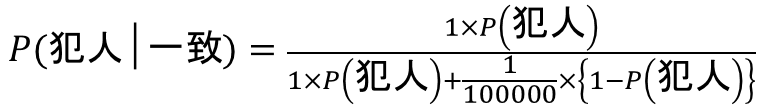
さて、ここでP(犯人)について考察してみましょう。事前情報が何もないため、犯人である確率を決めることができませんね。
①犯人であるか犯人でないの2通りなのだから、P(犯人) = 1/2
②この都市での殺人犯罪率は0.5%だから、P(犯人) = 5/1000
③この都市の人口は40万人だから、P(犯人) = 1/400000
などなど、事前確率P(犯人)は恣意的にいくらでも変えることができます。すると、事前確率P(犯人)で表すことのできるP(犯人│一致)も、恣意的に変化することになります。
A氏を犯人に仕立て上げようと思えば容易だし、犯人でないとするのもまた容易です。これでは使い物になりませんね。
→このような際には、ベイズの定理の使用を控えるべきです。
では、どうすれば恣意的な確率操作を減らすことができるのでしょうか。

こう考えると、X内に客観的データがたくさんあることで、P(X│A)やP(X)の相対的な比重が上がり、この計算におけるP(A)の影響が小さくなります。データ量を増やし、事前確率の影響を小さいものにすることで、恣意的な確率操作から計算結果を守ることができます。
4.ベイズ更新
最後に、よく使われている手法としてベイズ更新をご紹介いたします。
メールボックス内の迷惑メール対策など、様々な場面で実際に使われている手法です。
受信ボックスに届いたメールが
・迷惑メールである確率 A1
・迷惑メールではない確率 A2 とおきます。
メールの特徴B(事前確率)に基づいて、Aの事後確率を定義したとします。
ここで、さらに追加的なメールの特徴C(Bとは独立した情報)が得られた時、事後確率はどう変化するでしょうか。
![]()
これより、
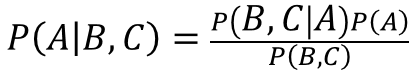
ここで、メールの特徴BとCは互いに独立した情報なので、
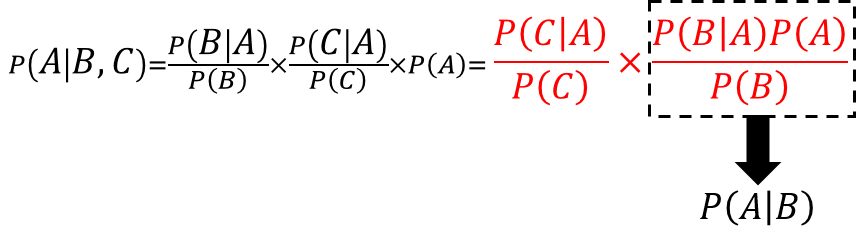
P(A│B)を情報Cに対しての事前確率分布とすると、
情報Bが与えられた際のAの事後確率を、新たなAの事前確率として新情報Cにベイズの定理を独立に適用している式となる。このような事象を「ベイズ更新」と呼びます。
実際の例で確認してみましょう。
受信ボックスに届いたメールAが
・迷惑メール A1
・迷惑メールでない A2
のどちらなのかを判定することにします。
メールAには、「完全無料」「必勝」「返信確実」「特典」が含まれていました。
日々飛び交っているメールのうち、70%のメールが迷惑メールだとします。P(A1) = 0.7
①
「完全無料」が含まれていたメールBが迷惑メールである確率が9%、迷惑メールでない確率が1%とすると、
P(B│A1) = 0.09
P(B│A2) = 0.01
このとき、「完全無料」が含まれているメールが迷惑メールである確率は、
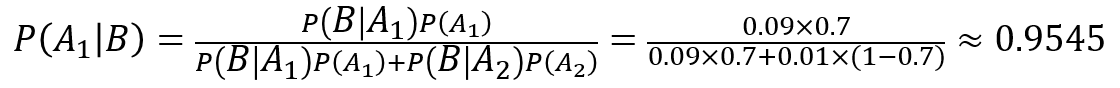
②
さらに、そのメールには「必勝」も含まれていた!このメールが迷惑メールである確率が11%、迷惑メールでない確率が2%とすると、ベイズ更新を利用して、
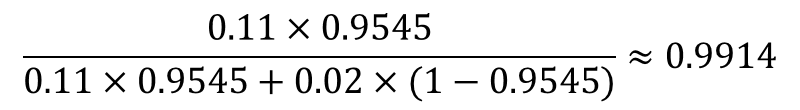
③
さらに、そのメールには「返信確実」も含まれていた!このメールが迷惑メールである確率は14%、迷惑メールでない確率が3%とすると、ベイズ更新を利用して、
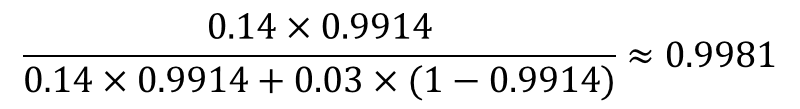
④
さらに、そのメールには「特典」も含まれていた!このメールが迷惑メールである確率は7%、迷惑メールでない確率が1%とすると、ベイズ更新を利用して、
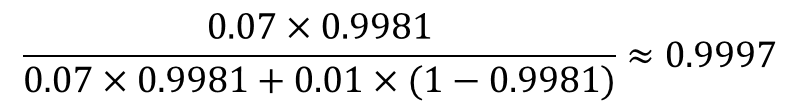
4回のベイズ更新で、迷惑メールでない確率は 0.06% と、かなり精度が上がっていることがわかります。
※但し、本来はメールにこの4つの単語が含まれるかは互いに独立ではないため、あくまでも近似的ですが、それでも十分にその威力を実感できるかと思います。
最後に
今回は、確率計算の基礎から、ベイズの定理の概要をお話しいたしました。この理論がベースとなって、機械学習は設計されています。実際になぜこのような理論が必要とされているのかは、また追ってご紹介できればと思います。数学が苦手だった方には苦痛な内容だったかもしれませんが、人工知能を十分理解できるかどうかの重要なポイントですので、しっかり押さえておきましょう。
(追記)
LINEのスタンプ、皆さんも一度は買ったことがあるのではないでしょうか。LINEスタンプのレコメンドエンジンに、ベイズ推定とDeep Learningが使用されているそうです。興味深いスライドでしたのでシェアさせていただきます!
-
お問い合わせ
SiTest の導入検討や
他社ツールとの違い・比較について
弊社のプロフェッショナルが
喜んでサポートいたします。 -
コンサルティング
ヒートマップの活用、ABテストの実施や
フォームの改善でお困りの方は、
弊社のプロフェッショナルが
コンサルティングいたします。
今すぐお気軽にご相談ください。
今すぐお気軽に
ご相談ください。
(平日 10:00~19:00)
今すぐお気軽に
ご相談ください。
0120-90-5794
(平日 10:00~19:00)
グラッドキューブは
「ISMS認証」を取得しています。

認証範囲:
インターネットマーケティング支援事業、インターネットASPサービスの提供、コンテンツメディア事業
「ISMS認証」とは、財団法人・日本情報処理開発協会が定めた企業の情報情報セキュリティマネジメントシステムの評価制度です。