A/Bテストの有意差とは?正しい判定方法からおすすめツールまで徹底解説
Webサイトの改善にA/Bテストは不可欠ですが、A/Bテストの結果を正しく解釈して次の施策に生かすことは簡単ではありません。専用のA/Bテストツールを導入すれば専門知識がなくても簡単かつ正確に結果を分析し、効果的なサイト改善を実現できます。
この記事ではA/Bテストにおける有意差の判定方法やおすすめの分析ツールを解説します。記事を読めばA/Bテストの結果に自信が持て、コンバージョン率向上につながるデータにもとづいた意思決定が可能です。
目次
ABテストとは2つの異なる要素を比較するテスト
 A/BテストはWebサイトや広告でAパターンとBパターンのどちらが良い成果を出すかを比較するテストです。担当者の勘や経験ではなく、実際のユーザーの反応データにもとづいて成果を判断できます。A/Bテストにより客観的に効果のある改善方法を見つけやすくなります。
A/BテストはWebサイトや広告でAパターンとBパターンのどちらが良い成果を出すかを比較するテストです。担当者の勘や経験ではなく、実際のユーザーの反応データにもとづいて成果を判断できます。A/Bテストにより客観的に効果のある改善方法を見つけやすくなります。
A/Bテストを活用し、コンバージョン率やクリック率などの指標を比較して効果的なデザインを判断しましょう。
» A/Bテストの基本とおすすめのA/Bテストツールを紹介!
有意差とはA/Bテスト結果が偶然ではないことを示す指標
 A/Bテストにおける「有意差」とはテスト結果の差が偶然ではなく、施策の効果による可能性が高いことを示す指標です。新デザインのクリック率が元デザインより高い場合、有意差があれば改善効果があると判断できます。
A/Bテストにおける「有意差」とはテスト結果の差が偶然ではなく、施策の効果による可能性が高いことを示す指標です。新デザインのクリック率が元デザインより高い場合、有意差があれば改善効果があると判断できます。
A/Bテスト結果に有意差がなければ、誤差の範囲内として判断されます。 有意差はテスト結果を正しく解釈するための重要な判断基準です。A/Bテストにおける有意差は効果のない施策を誤って採用するリスクを避けるために役立ちます。
» 総務省統計局「ウェブサイトの改善」(外部サイト)
A/Bテストにおける有意差の判定方法
 A/Bテスト結果を感覚的に判断すると間違った改善策を実行するリスクがあります。A/Bテストにおける有意差の判定方法は以下のとおりです。
A/Bテスト結果を感覚的に判断すると間違った改善策を実行するリスクがあります。A/Bテストにおける有意差の判定方法は以下のとおりです。
- 1.テスト期間を設定する
- 2.仮説を設定して検定方法を選択する
- 3.データを収集して整理する
①テスト期間を設定する
A/Bテストで正しい結果を得るには適切なテスト期間の設定が欠かせません。期間が短すぎたり長すぎたりすると正確なデータが取れず、判断を誤る原因になります。ユーザーの行動は曜日によって変わる傾向があります。
A/Bテストではユーザーの行動パターンの偏りをなくし、公平なデータを集めなければなりません。 サイトへの訪問者が少ない場合、十分なデータが集まるまでテスト期間を長めに設定します。セールや大型連休、給料日の前後などユーザーの行動が通常と大きく異なる期間は、A/Bテストは避けてください。
高額な商品や法人向けサービスなどの購入までに時間がかかるものは、テストを長く行いましょう。 A/Bテスト期間中は結果が変動しやすいため、統計的有意性を慎重に判断する必要があります。
事前に設定したサンプルサイズに達するか、統計的に有意な結果が確認できるまでデータを収集し続けましょう。ただし、明確な統計的有意差が確認できた場合は事前に決めた期間を待たずに判断することも可能です。
②仮説を設定して検定方法を選択する
 A/Bテストの結果を正しく評価するには事前に具体的な仮説を立て、仮説を検証するための検定方法を選択しましょう。仮説がないテストは、結果に至った経緯を分析できないため次の改善に生かせません。
A/Bテストの結果を正しく評価するには事前に具体的な仮説を立て、仮説を検証するための検定方法を選択しましょう。仮説がないテストは、結果に至った経緯を分析できないため次の改善に生かせません。
A/Bテストを行う際は「帰無仮説:A案とB案に差はない」と「対立仮説:A案とB案には差がある」という2つの仮説を設定し、統計的検定によって帰無仮説を棄却できるかを判断します。 A/Bテスト結果が偶然ではないと判断するための基準(有意水準)もあらかじめ決めておきましょう。
有意水準は5%に設定されることが一般的です。コンバージョン率などの割合のデータを比べるのか、サイトの滞在時間などの平均値を比べるのかで適切な検定手法が異なります。
» 総務省統計局「統計的推定と統計的仮説検定」(外部サイト)
③データを収集して整理する
A/Bテストでどちらのデザインが良いかを正しく判断するには、データ収集とデータ整理が大切です。正確なデータがなければ、どちらのパターンが本当に優れているのかを科学的に判断できません。A/Bテストを行う際はテストするデザインごとに以下の情報を集めて整理しましょう。
- ・Aパターン・Bパターンなど、テストするデザインを決める
- ・各デザインを閲覧したユーザー数を計測する
- ・各デザインで目標(例:商品の購入)を達成したユーザー数を計測する
- ・収集したデータから各デザインの成果(コンバージョン率)を算出する
サイトのデザインごとに見た人の数と目標を達成した人の数を並べて比較できるようにしてください。
統計的検定で知っておくべき用語
 A/Bテストの結果を正確に解釈するためには以下の統計的検定の基本用語を理解しましょう。
A/Bテストの結果を正確に解釈するためには以下の統計的検定の基本用語を理解しましょう。
| 用語 | 説明 |
|---|---|
| 帰無仮説 | 「効果がない」「差がない」など、 否定的な仮説。 統計的検定で検証の対象となる仮説 |
| 対立仮説 | 帰無仮説に対立する仮説。 検証したい、証明したい仮説 |
| 棄却 | 仮説が間違っていることを判断すること |
| 第一種の過誤 | 帰無仮説が正しいにも関わらず 帰無仮説を棄却すること |
| 第二種の過誤 | 対立仮説が正しいにも関わらず 帰無仮説を棄却しないでいること |
| p値 | 帰無仮説のもとで実際にデータから計算された統計量よりも 極端な(仮説に反する)統計量が観測される確率 |
「帰無仮説を棄却し、対立仮説が妥当と判断されるか」がA/Bテスト結果を採用する際の基準です。仮説検定はあくまで確率論であるため、合理的な判断であっても真実とは限らないことを理解しておきましょう。 「差があるか」を方向性に関係なく検証したい場合は両側検定を行います。
「良くなる」または「悪くなる」など特定の方向性に絞って検証したい場合は、片側検定を選択してください。両側検定と片側検定は仮説検定における対立仮説の立て方の違いを指します。
A/Bテストで用いる4つの統計検定手法
 A/Bテストで用いる以下の4つの統計検定手法を解説します。
A/Bテストで用いる以下の4つの統計検定手法を解説します。
- ・二項検定
- ・t検定 (t-test)
- ・カイ二乗検定 (Chi-square test)
- ・ベイズ検定 (Bayesian test)
二項検定
A/Bテストで用いる統計検定手法の一つに二項検定があります。二項検定はA/Bテスト結果が2つの選択肢のみの事柄について、どちらのパターンに効果があるかを判断する分析方法です。WebサイトのA/Bテストでは、はっきりとした2択の結果を比べる際に二項検定がよく使用されます。
二項検定はボタンの色やキャッチコピーなどの2つのパターンを比べて、より高い成果を出す方を統計的に判断する際に役立ちます。二項検定ではそれぞれのユーザーの行動が他のユーザーに影響を与えないことが前提です。
A/Bテストでは二項検定のほか、データの性質に応じてt検定やZ検定などの統計手法が使用されています。 多くのA/Bテストツールには二項検定やt検定、Z検定などの統計手法が組み込まれており、A/Bテスト結果の解釈が容易になっています。
t検定 (t-test)
 t検定は2つのグループの平均値に意味のある差があるかを判断するための手法です。Webサイトのデザインを変更した際、変更前後で平均購入単価や平均滞在時間に本当に差が出たのかを確かめるときに役立ちます。
t検定は2つのグループの平均値に意味のある差があるかを判断するための手法です。Webサイトのデザインを変更した際、変更前後で平均購入単価や平均滞在時間に本当に差が出たのかを確かめるときに役立ちます。
A/Bテストでは結果が単なる偶然の誤差なのか、施策によって生まれた意味のある差なのかを統計的に証明しなければなりません。t検定をA/Bテストに用いるとテスト結果の差が客観的に見て意味を持つものかを判断できます。 t検定はサイトの平均滞在時間やセッション当たりの平均ページ閲覧数など、連続した数値データの平均値を比較する際に有効です。
ただし、コンバージョン率のような比率で表されるデータの比較には比率の差の検定や、データを適切に変換してからt検定を行う方法が推奨されます。 t検定を使用するにはデータが正規分布に従うなどの前提条件を満たす必要があります。
t検定はWebサイトの改善効果測定を含むさまざまな分野で、データにもとづいた客観的な判断を行うために広く使用される検定手法です。
カイ二乗検定 (Chi-square test)
カイ二乗検定はカテゴリデータ(アンケートの選択肢や商品の購入有無など)において、観測された頻度と理論的に期待される頻度との差が統計的に有意かを判断するための手法です。
適合度検定では複数のカテゴリが理論分布に従うかを、独立性の検定では2つ以上のカテゴリ変数間に関連があるかを検証できます。 連続値や量的データの平均値の差を検定する場合は、t検定や分散分析(ANOVA)などの手法を活用してください。
カイ二乗検定では帰無仮説として「観測されたデータが期待される分布と一致する」という仮説を立てます。 仮説のもとで観測データと期待データを比較し、比較結果のズレの大きさからデータ間に有意な差があるかどうかを判定しましょう。
ベイズ検定 (Bayesian test)
ベイズ検定はベイズの定理を用いて事前情報と観測データを組み合わせ、各パターンの効果の確率分布を推定する手法です。SiTestをはじめとする多くのA/Bテストツールでは、ベイズ検定が採用されています。
A/Bテストにおいて、結果を確率的に解釈できるため不確実性を考慮した柔軟な意思決定が可能です。 データが集まるごとに事後確率を更新する段階的なアプローチが可能なベイズ検定は、リアルタイムでの意思決定をサポートします。
ベイズ検定は過去のテスト結果や経験などの「事前の情報」を分析に含めることも可能です。ベイズ検定を用いるとA/Bテストの途中でも優劣の確率を確認できるため、機会損失を減らせます。 結果がわかりやすく、A/Bテスト運用における柔軟性が高い点がベイズ検定のメリットです。
» 機械学習の理解に必須!ベイズ統計学の基礎の基礎
A/Bテストの実施から有意差判定までのツール活用フロー

A/Bテストを効果的に行うには、適切なツールを活用した体系的なアプローチが必要です。A/Bテストの実施から有意差判定までツールの活用フローは以下のとおりです。
- 1. 目的と仮説を明確にする
- 2. A/Bテスト内容と指標を設定する
- 3. A/Bテストを実施し、データを分析する
- 4. 結果を判断して改善に活かす
目的と仮説を明確にする
A/Bテストを始める前に、何を改善したいのか、どんな仮説を検証したいのかを明確にすることが重要です。明確な目的と仮説がなければ、テストの結果が判断しにくく、改善につなげられません。 ビジネス目標に直結したA/Bテストの計画を立てることで、効果的な改善につながります。
A/Bテストを実施するために、以下のような改善したいビジネス目標を具体的に設定しましょう。
- ・コンバージョン率の向上
- ・クリック率(CTR)の改善
- ・ユーザー滞在時間の延長
- ・離脱率の低減
現状の問題点や課題を特定し、データ分析やユーザーフィードバックから、改善が必要な部分を明らかにすることが大切です。問題点や課題を踏まえて「もし〜すれば、〜になるだろう」という形で具体的な仮説を立てます。
仮説は必ず測定可能で検証可能な形にし、曖昧な表現ではなく、数値目標を含めましょう。複数の仮説がある場合は、ビジネスへの影響度や実装の容易さなどを考慮して優先順位をつけることをおすすめします。
A/Bテスト開始前に、仮説に基づいた変更点を明確に定義し、期待される効果を数値目標として設定します。A/Bテストの実施期間と必要なサンプル数を見積もってください。十分なデータ量を確保するためには、適切なA/Bテストの期間設定が不可欠です。
A/Bテスト内容と指標を設定する
A/Bテストの内容と指標の設定を曖昧にすると正確な結果が得られないため、計画段階でしっかりと準備しましょう。まずA/Bテストの対象となる要素を具体的に決めます。
ヘッドラインやCTAボタン、画像、レイアウトなど、変更したい部分を明確にしたうえで、A版(現状)とB版(テスト版)の違いを細かく定義してください。 次に測定する指標を設定します。主要指標(KPI)として以下のようなものが考えられます。
- ・クリック率
- ・コンバージョン率
- ・滞在時間
- ・離脱率
- ・平均注文額
A/Bテストの信頼性を高めるためには、統計的有意性を担保するサンプルサイズを事前に計算しておくことも大切です。A/Bテストのサンプル数が少なすぎると偶然の結果を誤って採用してしまう可能性があります。テスト期間は最低でも1〜2週間は確保し、季節変動なども考慮しましょう。
A/Bテストの実施前にトラッキングコードやタグの設置を確認し、デバイス間での表示の違いも考慮してください。デバイスタイプや地域、新規/リピーターなどのセグメント分析の準備もしておくと、より深い洞察が得られます。
A/Bテストを実施し、データを分析する

A/Bテストを始めたら、データ収集と分析をして十分な情報を集め、正確な判断ができるようにしましょう。A/Bテストの期間はサイトのトラフィック量や期待する効果量に応じて、一般的には1〜4週間程度を目安に設定します。
A/Bテストツールを使って、コンバージョン率やクリック率、滞在時間、離脱率などの重要な指標を測定してください。データ分析では統計的有意性を確認し、p値が0.05未満であれば、統計的に有意と判断されます。異常値や外れ値がないかも確認し、必要に応じてデータクリーニングを行いましょう。
定量的なデータだけでなく、ユーザーからの感想やフィードバックなどの定性的な情報も集めると、より総合的な判断が可能です。
結果を判断して改善に活かす
A/Bテストを実施した後は、統計的有意差に基づいて勝者バリエーションを決定することで、より確実な成果を得られます。A/Bテストの結果が出たら、まずは統計的な有意差があるかどうかを確認してください。有意差がある場合は、バリエーションを本番環境に実装するかどうかを判断します。
しかし、単に数字だけでなく、ビジネス全体の目標や方向性も考慮する必要があります。予想と異なる結果が出た場合は、新たな発見や洞察が得られることもあるため、以下のポイントを確認しましょう。
- ・A/Bテストの期間
- ・サンプルサイズ
- ・外部要因
- ・ユーザー層
A/Bテストの結果から得られた洞察は組織内で共有することで、チーム全体の知識が蓄積され、次のテスト仮説の立案に役立ちます。小さな改善でも継続的に積み重ねることで、長期的には大きな効果につながります。1回のA/Bテストで劇的な改善が見られなくても、諦めずに継続することが重要です。
A/Bテストの結果はビジネスKPIに換算して価値を可視化すると、経営層や他部署にもその重要性を理解してもらいやすくなります。A/Bテスト終了後も長期的な効果を測定するために継続的にモニタリングしましょう。複数のA/Bテスト結果を組み合わせて分析することで、より包括的な改善戦略を構築できます。
有意差を判定するA/Bテストツールの選び方
 有意差を判定するA/Bテストツールを選ぶ際は以下を参考にしてください。
有意差を判定するA/Bテストツールを選ぶ際は以下を参考にしてください。
- ・目的に合っているか
- ・A/Bテストツールの費用が適切か
- ・サポート体制が整っているか
上記の基準をもとに、最適なツールを選ぶための「A/Bテストツール選び方ガイド」を無料で配布しています。ツール選定でお悩みの方は、ぜひ下記よりダウンロードしてご活用ください。
目的に合っているか
A/Bテストツールを選ぶ際は自社の目的や課題を解決できる機能がそろっているかを確認しましょう。サイトのコンバージョン率を上げたい、ユーザーの行動を詳しく知りたいなど、解決したい課題を明確にしてください。A/Bテストツールを選ぶ際は以下の機能が自社に必要かを確認してから選択しましょう。
- ・課題解決機能
- ・ヒートマップなど分析機能
- ・パーソナライズ機能
- ・導入・操作の簡易性
- ・テスト対応範囲
- ・外部ツールとの連携
自社のWebサイト運営の目的に合ったA/Bテストツールを選ぶことが、成果を出すための近道です。
A/Bテストツールの費用が適切か
 A/Bテストツールを選ぶ際は料金の安さだけで決めず、自社のサイト規模やテストの頻度に合っているかで判断しましょう。ツールによって料金の仕組みが大きく異なります。一見安く見えてもサイトのアクセス数が増えると料金が跳ね上がったり、必要な機能が有料オプションだったりする場合があります。 A/Bテストツールの費用を正しく比較するには以下の点を確認しましょう。
A/Bテストツールを選ぶ際は料金の安さだけで決めず、自社のサイト規模やテストの頻度に合っているかで判断しましょう。ツールによって料金の仕組みが大きく異なります。一見安く見えてもサイトのアクセス数が増えると料金が跳ね上がったり、必要な機能が有料オプションだったりする場合があります。 A/Bテストツールの費用を正しく比較するには以下の点を確認しましょう。
- ・料金体系
- ・トータルコスト
- ・無料プランの制限
- ・契約条件
複数のA/Bテストツールを比較し、自社に最適なコストパフォーマンスの高いツールを選びましょう。
サポート体制が整っているか
高機能なA/Bテストツールを導入しても操作方法がわからなかったり、分析でつまずいたりするとA/Bテストが進まなくなります。知識に自信がない担当者でも手厚いサポートがあれば安心してツールを使いこなせます。A/Bテストツールを選ぶ際は以下の点を確認しましょう。
- ・導入時の初期設定や実装をサポートしてくれるか
- ・メールや電話、チャットなどの問い合わせ方法が充実しているか
- ・専任の担当者によるサポートがあるか
- ・施策の立案や分析レポート作成といったコンサルティングを受けられるか
- ・海外のツールの場合、日本語でのサポートに対応しているか
- ・使い方を学べるマニュアルやセミナーが充実しているか
サポートが手厚いA/Bテストツールを選べばスムーズにサイト改善を図れます。
A/Bテストで有意差を正確に出すポイント4選
 A/Bテストで有意差を正確に出すポイントは以下の4つです。
A/Bテストで有意差を正確に出すポイントは以下の4つです。
- ・A/Bテスト対象をしっかり分析してから仮説を立てる
- ・A/Bテストの変数を1つに絞る
- ・適切なA/Bテスト期間を選定する
- ・十分なサンプルデータを収集する
A/Bテスト対象をしっかり分析してから仮説を立てる
A/Bテストで正確な結果を得るにはテストを始める前に対象をしっかり分析し、データにもとづいた仮説を立てることが大切です。分析をせずに勘や思いつきでテストを始めると改善の根拠が不明確になり、成果が出にくくなります。
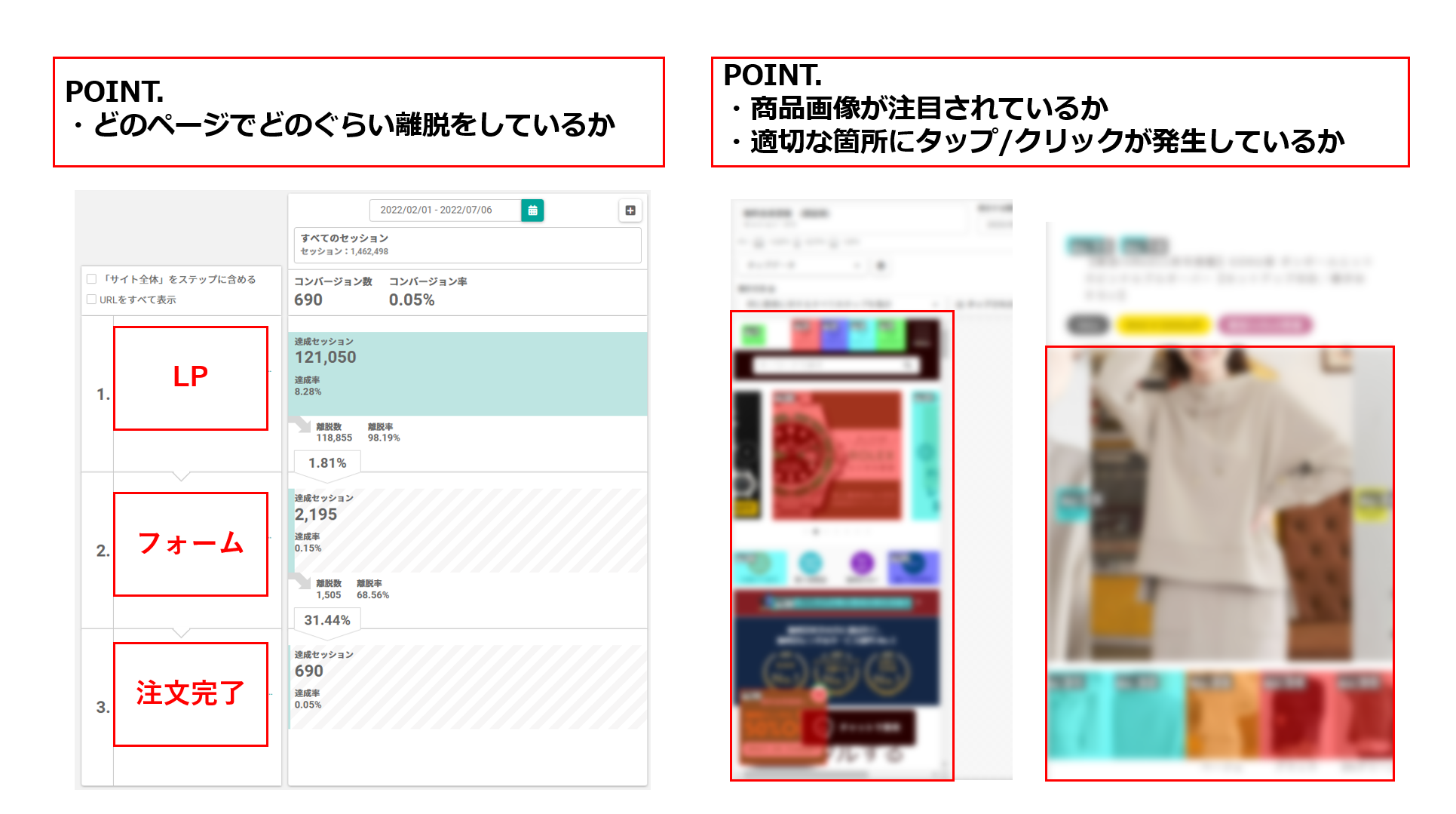
サイト解析ツールを使うとデータにもとづいた客観的な分析ができます。 アクセス解析で離脱率が高いページやクリック率が低いボタンといった問題箇所を見つけましょう。ヒートマップでユーザーがページのどこをよく見て、どこで離脱しているかを視覚的に確認します。
セッションリプレイではユーザーの実際の操作を録画再生し、フォーム入力でのつまずきや迷いの原因を探りましょう。 A/Bテスト対象をしっかり分析するとデータに裏付けされた論理的な仮説を立てられます。
A/Bテストの変数を1つに絞る
A/Bテストで成果を正確に測るには変更する箇所を1つに絞りましょう。A/Bテストの際に複数の場所を同時に変更すると、どの変更が成果に影響したのか原因がわからなくなるためです。
正確な原因をA/Bテストで突き止めるには最も影響が大きいと仮説を立てた1つの要素に絞ってテストしてください。 変更点を1つに絞り込むことで何が効果的だったのかを正確に把握でき、再現性のある改善につなげられます。
適切なA/Bテスト期間を選定する
 A/Bテストは期間が短すぎても長すぎても正しい結果が得られないため最低1週間、可能であれば2〜4週間行いましょう。テスト期間が長すぎると市場のトレンド変化や季節的な要因の影響を受け、テストの純粋な効果を測りにくくなります。
A/Bテストは期間が短すぎても長すぎても正しい結果が得られないため最低1週間、可能であれば2〜4週間行いましょう。テスト期間が長すぎると市場のトレンド変化や季節的な要因の影響を受け、テストの純粋な効果を測りにくくなります。
信頼できるデータを集めるためには最低でも1週間単位でA/Bテストを実施してください。曜日ごとの行動パターンの偏りをなくすため、7の倍数の日数で設定しましょう。自社サイトの特性や状況を考慮して期間を設定することが、A/Bテストの精度を高めるための重要なポイントです。
十分なサンプルデータを収集する
A/Bテストで信頼できる結果を得るには十分なサンプルデータを集めましょう。ユーザー数が少ないと結果が偏りやすく、改善案の効果を正確に見極めることが難しくなります。各パターンで最低でも50コンバージョン、5,000~1万セッションが目安です。
より正確なデータ量を知りたい場合はオンラインで無料で使える「サンプルサイズ計算ツール」を活用しましょう。計算ツールでは現在のコンバージョン率や期待する改善率、有意水準(通常は5%)の情報を入力します。
事前に設定したサンプルサイズに達するまで、途中の結果が良くても悪くてもテストを止めないでください。 計画的に十分なデータを集めることでA/Bテストの精度を向上させられます。
A/Bテスト結果に有意差が出ない場合の対処法

A/Bテスト結果に有意差が出ない場合の対処法を以下のケースごとに解説します。
- ・変化量が少ない場合の対策
- ・サンプル数が少ない場合の対策
- ・A/Bテスト期間が不十分な場合の対策
変化量が少ない場合の対策
A/Bテストで試した内容の変化が小さすぎるとユーザーの行動に影響が出にくく、結果として有意差が出ない場合があります。変化量が少ない場合はより大胆でわかりやすい内容に変更しましょう。
ユーザーが変更点に気づかなければユーザーの行動も変わりません。 はっきりと違いがわかるA/Bテストを行うことでユーザーの反応を確かめられます。根本的な課題を再分析したり、多変量テストを検討したりすると有意差を検出可能です。
A/Bテストを行う際に中間目標を設定するとテストの進捗状況の把握が容易になり、改善点を早期発見できる場合があります。 小さな変更で差が出ないときは思い切って大きな変更を加えると、ユーザーの心に響く改善点を見つけ出せます。
» 多変量テストの基礎知識や具体的な実施・分析方法を解説
サンプル数が少ない場合の対策
 サンプル数が少ない場合はテストのやり方を見直すことで、少ないデータでも意味のある結果を得やすくなります。アクセス数が限られるサイトでは十分なサンプルを集めること自体が課題になるケースもあります。
サンプル数が少ない場合はテストのやり方を見直すことで、少ないデータでも意味のある結果を得やすくなります。アクセス数が限られるサイトでは十分なサンプルを集めること自体が課題になるケースもあります。
サンプル数が少ない場合は、CTAのクリック数やページ到達数など、コンバージョンにつながる手前のアクションをマイクロコンバージョンとして設定しましょう。
Webサイトのテキストや色の微修正ではなく、デザインのレイアウトや訴求の軸を大きく変更するテストを行うことも有効です。
ベイズ統計のツールを利用すると事前情報を活用して推定を行えます。しかし、サンプルサイズが小さい場合は結果の不確実性が高まるため注意が必要です。
» A/Bテストのサンプル数に必要な要素や計算方法を解説
A/Bテスト期間が不十分な場合の対策
A/Bテストの期間が短すぎて正確な結果が得られない場合、テスト期間を見直したりテストのやり方を工夫したりしましょう。2週間以上のテスト期間が一般的に推奨されています。曜日ごとの行動の違いを考慮し、最低でも1週間のデータを集めて全体のトレンドを把握することが重要です。
Webサイトの中でも特に多くの人が訪れるページでテストをすれば、短期間でもデータを集めやすくなります。デザインやキャッチコピーを大きく変えるなどの大胆な仮説を試すと短期間でも反応の差が出やすくなります。
新規訪問者や特定の広告から来た人など、対象者を限定してテストを実施することも一つの方法です。
» A/Bテストの最適な期間と期間を決める6つの要素
A/Bテストと有意差に関するよくある質問
 A/Bテストと有意差に関するよくある質問は以下のとおりです。
A/Bテストと有意差に関するよくある質問は以下のとおりです。
- ・有意差があるのにコンバージョンがあまり変わらないのはなぜ?
- ・有意差の有無で施策を実行する判断基準は?
- ・無料のツールの有意差の判定は信用できる?
有意差があるのにコンバージョンがあまり変わらないのはなぜ?
統計上の有意差は必ずしもビジネスにおける大きな成果を意味するわけではありません。有意差はテスト結果の差が「偶然ではない」ことを示す指標であり、効果の大きさそのものを保証するものではないためです。
ごくわずかな差であってもA/Bテストに参加したユーザー数が多ければ、統計的に有意な差として検出されます。 わずかなコンバージョン率の改善でも有意差は出ます。しかし、実際のコンバージョン数に換算するとほとんど差がないように見える場合があるため注意が必要です。
サイト訪問者全体で見ると改善していても、売上に大きく貢献する優良顧客など特定の顧客層には響いていない可能性があります。 A/Bテスト期間中のイベントや競合他社のキャンペーンなどがサイト全体のコンバージョン数に影響を与える場合もあります。
施策のコストが見合っていないことも有意差があるのにコンバージョンがあまり変わらない原因の一つです。 施策を実行・維持するためのコストを考慮すると改善によって得られる利益が相殺される恐れもあります。
A/Bテストでは有意差だけを見るのではなく、コンバージョン数の変化や利益への影響度などを総合的に見て判断しましょう。
有意差の有無で施策を実行する判断基準は?
 A/Bテストの結果で有意差が出たとしても施策を実行するべきとは限りません。統計的な結果だけでなく、ビジネス全体への影響やコストを総合的に見て判断しましょう。施策の実行にはデザインの変更やシステムの改修など、さまざまなコストがかかる場合があります。
A/Bテストの結果で有意差が出たとしても施策を実行するべきとは限りません。統計的な結果だけでなく、ビジネス全体への影響やコストを総合的に見て判断しましょう。施策の実行にはデザインの変更やシステムの改修など、さまざまなコストがかかる場合があります。
改善によって得られる利益が施策にかかる費用や手間を上回らなければ、ビジネスとしては意味がありません。施策の実行を検討する際は費用対効果を慎重に分析し、期待される利益が投資コストを上回る場合に施策を実行してください。
利益が費用と同程度の場合はデザインの好みやブランドイメージとの整合性、長期的な戦略への適合性なども考慮しましょう。コンバージョン率が上がっても客単価が下がってしまうなど、他の数字が悪化していないかも確認します。
全体では有意差がなくても、スマートフォンからの訪問者や新規の訪問者だけで良い結果が出ている場合があります。一部のユーザー層に限定して施策を実行することも一つの手です。有意差はあくまで判断材料の一つです。
施策がビジネス全体の目標達成に本当に役立つのかという視点で判断しましょう。
無料のツールの有意差の判定は信用できる?
無料のA/Bテストツールが出す有意差の判定は基本的なテストの範囲であれば信用できます。多くの無料ツールは広く使われている標準的な統計の考え方にもとづいて結果を計算しているためです。しかし、どのように数値を算出しているか計算方法がわからないツールもあります。
無料のA/Bテストツールは機能が限られている場合が多く、複雑なテストには対応していないケースがほとんどです。多くの人が訪れるサイトや会社の売上に直接関わる重要なテストを行う場合は、有料のA/Bテストツールの利用がおすすめです。
無料ツールでA/Bテストに慣れて、より深く正確な分析が必要になったときに有料ツールへの移行を検討しましょう。
A/Bテストの有意差を簡単・正確に判定するなら「SiTest」がおすすめ!

Webサイトの成果を高めるには、A/Bテストツールの活用が欠かせません。中でも「SiTest(サイテスト)」は、統計の専門知識がなくてもA/Bテストの有意差を簡単に確認できます。正確な検証には適切な仮説設定や十分なテスト期間などの統計的配慮も重要ですが、SiTestなら初心者でも安心して取り組めます。
SiTestはA/Bテストだけでなく、ヒートマップやEFO(エントリーフォーム最適化)などの機能も一体化されており、効率的な改善サイクルの構築をサポート。自社の目的や予算に合った導入がしやすく、GA4との連携もできます。
国産のツールのため、専任のサポートによる支援が受けられる点も評価が高いポイントです。本格的にWebサイトの改善を進めたい方にとって、機能・サポートともに充実したSiTestは心強い選択肢となります。
-
お問い合わせ
SiTest の導入検討や
他社ツールとの違い・比較について
弊社のプロフェッショナルが
喜んでサポートいたします。 -
コンサルティング
ヒートマップの活用、ABテストの実施や
フォームの改善でお困りの方は、
弊社のプロフェッショナルが
コンサルティングいたします。
今すぐお気軽にご相談ください。
今すぐお気軽に
ご相談ください。
(平日 10:00~19:00)
今すぐお気軽に
ご相談ください。
0120-90-5794
(平日 10:00~19:00)
グラッドキューブは
「ISMS認証」を取得しています。

認証範囲:
インターネットマーケティング支援事業、インターネットASPサービスの提供、コンテンツメディア事業
「ISMS認証」とは、財団法人・日本情報処理開発協会が定めた企業の情報情報セキュリティマネジメントシステムの評価制度です。
































