ランプの魔人「Akinator」でも使われている!ベイズの定理とは?
全世界で遊ばれているゲーム「Akinator」をご存知でしょうか。少し前に流行りましたよね。
20個ほどの質問内容に回答すると、ユーザーが想像した実在または架空の人物・キャラクターをズバリ言い当ててしまうアプリケーションです。
Aknatorの内部構造は非公開ですが、質問を繰り返す点や答えられない場合は新たに質問を追加していき日々学習を繰り返す点など、まさしく人工知能であると言えます。
今回はそんなAkinatorでも内部のロジックとして使用されている(と言われている)統計学の一種「ベイズ統計学」の基となった定理「ベイズの定理」についてご紹介します。
ベイズの定理とは?
ベイズの定理(ベイズのていり、英: Bayes’ theorem)とは、条件付き確率に関して成り立つ定理で、トーマス・ベイズによって示された。
なおベイズ統計学においては基礎として利用され、いくつかの未観測要素を含む推論等に応用される。
Wikipedia:ベイズの定理
条件付き確率とは?
条件付き確率というのは、特定の条件Yが発生している基で条件Xが発生する確率です。
数式ではP(x|y)と表します。
例えば
トランプの山(52枚)から1枚目にスペードを、
そのカードを戻さずに2枚目にダイヤを引く確率
という例題で考えてみましょう。
中学の数学で出てきたような問題っぽいですよね。
1枚目がスペード・・・条件Y
2枚目がダイヤ・・・条件X
となります。
1枚目がスペードな確率は
P(x) = 13/52 = 1/4
2枚目がダイヤな確率は山から1枚目のカードがない状態(51枚)ですので
P(y) = 13/51
となります。
よって条件Xが発生しているもとで条件Yが発生する確率 P(x|y)は
P(x|y) = 1/4 * 13/51 = 13/204
となります。
なんとなくご理解していただけたでしょうか。
ベイズの定理
P(x)P(y|x) = P(y)P(x|y) = P(x∩y)
P(x):事象Xが起きる確率
P(y|x):事象xが起きたもとで事象yが起きる確率
P(x∩y) :事象xと事象yが両方発生する確率(xとyの積集合)
x側から考えると
P(x)P(y|x) = P(x∩y)
同様にy側から考えると
P(y)P(x|y) = P(y∩x)
よって以下の恒等式
P(x)P(y|x) = P(y)P(x|y)
が成立します。
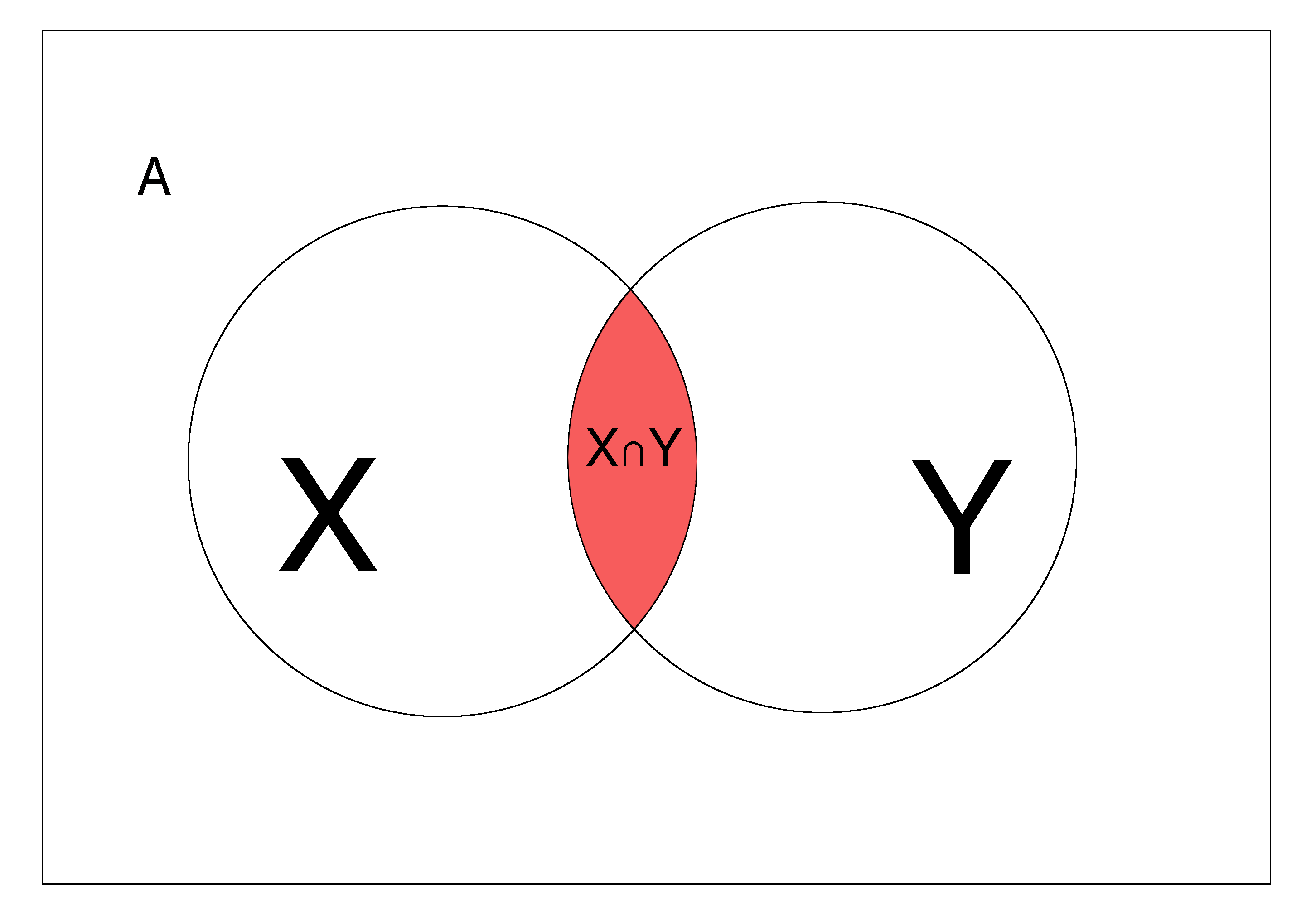
「ベイズの定理とはベン図の両側から攻めてP(x∩y)を2通りの方法で表したもの」と言えます。
一般的には条件付き確率を求めるために
P(y|x) = P(y)P(x|y) / P(x)
の形で使われることが多いです。
まとめ
今回は確率の公式からベイズの定理を導くところまでご説明しました。
Akinatorでも利用されているかはわかりませんが、事象(回答)を重ねていき、正解への確度を上げていくようなロジックは、さらに機械学習と交ぜることにより、Akinatorのような高度な人工知能が出来上っても不思議ではありません。
次回はベイズ更新からベイズ推定の解説をしたいと思います。
ベイズ統計に入門して、ベイジアンになりましょう!
-
お問い合わせ
SiTest の導入検討や
他社ツールとの違い・比較について
弊社のプロフェッショナルが
喜んでサポートいたします。 -
コンサルティング
ヒートマップの活用、ABテストの実施や
フォームの改善でお困りの方は、
弊社のプロフェッショナルが
コンサルティングいたします。
今すぐお気軽にご相談ください。
今すぐお気軽に
ご相談ください。
(平日 10:00~19:00)
今すぐお気軽に
ご相談ください。
0120-90-5794
(平日 10:00~19:00)
グラッドキューブは
「ISMS認証」を取得しています。

認証範囲:
インターネットマーケティング支援事業、インターネットASPサービスの提供、コンテンツメディア事業
「ISMS認証」とは、財団法人・日本情報処理開発協会が定めた企業の情報情報セキュリティマネジメントシステムの評価制度です。