ABテストの終わりを見極める！統計的有意差と仮説検定入門 ｜ SiTest (サイテスト) ブログ

ウェブサイト改善のためにABテストを行った際に、何を基準にABテストを終えられていますか？
「十分なインプレッションが集まったら」
「コンバージョン数やコンバージョン率に明らかな差がついたら」・・・こんな感じでしょうか。
しかし、この「十分な」「明らかな」という言葉の定義は非常に曖昧です。

実は、この曖昧な言葉の根拠とすべきものが「仮説検定」というものです。
仮説検定で十分な統計的有意差を得られるだけのデータが集まれば、それで終了して良いのです。
今回は、仮説検定について紐解きながらA/Bテストの終わり時を考えてみたいと思います。
また、SiTest 内にも仮説検定に代わる支援機能がありますので併せてご紹介いたします！

【Index】
１．仮説検定とは？
２．ABテストと仮説検定の関係性
３．仮説検定をやってみよう
４．SiTest にある支援機能

今回ご紹介するのは、仮説検定、あるいは統計学的仮説検定と呼ばれるものです。
（詳しく学びたいという方は、芝浦工大「確率と統計」の教科書をご参照いただくと良いと思います。）

ざっくりと言いますと、
とある「仮説」を立て、その「仮説」が正しいと言ってしまってよいかを統計学的・確率論的に判断するための方法です。
とても回りくどいのですが、

「仮説」が正しいとの仮定のもと、その仮説に従う母集団から実際に観察された標本を抽出される確率を求める。
その確率が、予め決めておいた確率値より”十分に”小さければ、その「仮説」が限りなく誤りに近いものだ、と判断する。

というやり方で行います。
では、一体この仮説検定、ABテストと何の関係があるのでしょうか？

ランディングページから商品の購入を促したいと考えているとします。
そのために、購入を促す画像を2種類用意し、どちらが良いかテストしてみることにしました。

A：購入を促す女性の画像
B：購入を促す男性の画像

同じクリック数までテストした時、次のような結果が得られたとしましょう。

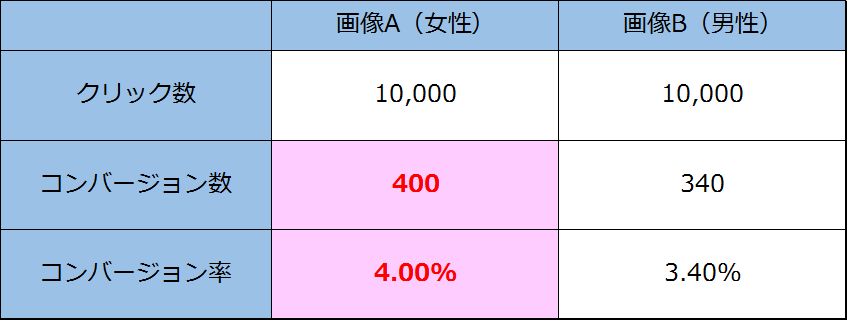
Aの画像のほうが、同じクリック数でコンバージョン（購入）が多かったようです。
この結果を見て、Aの画像のほうがユーザーに受け入れられたと言えるのでしょうか。
それとも、この結果は単なる偶然なのでしょうか。
その問いに、統計学的に結論を出すことができるのが「仮説検定」という方法なのです。

結果が偶然ではないことを証明するために立てる仮説を「帰無仮説」と言います。
先程の例で言えば、
証明したい仮説：画像Aと画像Bにはコンバージョン数の差異を決定づける明らかな差が「ある」
帰無仮説：画像Aと画像Bにはコンバージョン数の差異を決定づけるほどの明らかな差が「ない」
となります。

A, Bの2つの画像に特別な違いがないにもかかわらずコンバージョン数が違う結果になるようなことは「偶然」であり、
「滅多と起こらない」ことだと仮説検定によって言うことができれば、

「滅多と起こらない」ことが起こるはずがない
　→ 帰無仮説が誤りであった可能性が極めて高い
　→ 証明したい仮説は正しい可能性が極めて高い
　→ 画像Aの方が効果があった可能性が極めて高い

とロジカルに結論付けられることになります。

ここで、実際の計算に入る前に、一つ重要な指標のお話を。
「有意水準」
～ある事象が、「十分起こりうる」と「滅多と起こるはずがない」の境界の確率。
　有意水準5%＝5%以下の確率でしか起こらないような事象は、「滅多と起こるはずがないもの」とみなす。

例えば、コインを10回投げて表が何回出るかというテストをしたとしましょう。
有意水準を5%に設定すると・・・
・１０回とも表が出る確率＝1/1024≒0.00098（0.098%）<5%　「滅多と起こるはずがない」
・９回以上表が出る確率＝(101)/1024+1/1024≒0.018（1.8%）<5%　「滅多と起こるはずがない」
・８回以上表が出る確率＝(109/2)/1024+(10*1)/1024+1/1024≒0.055（5.5%）>5%　「十分起こりうる」
そもそも、この確率の計算は「コインはどこにでもある表裏が50%ずつ出るコイン」という仮定＝帰無仮定でされており、
それが「滅多と起こるはずがない」結果になったら、帰無仮定は誤りである可能性が高いとみなします。
よって、９回以上表が出たら「このコイン自体が細工されているものである可能性が高い」と結論付けられるのです。

では、実際に計算をしてみることにしましょう。

【今回のケース】
画像A：クリック数 10,000、コンバージョン数 400
画像B：クリック数 10,000、コンバージョン数 340

前述のコイン投げの検定のように一つ一つ計算していっても良いのですが、
あまりにも計算量が膨大なので、今回は「比率の差の検定」というものを使って仮説検定を進めます。
「比率の差の検定」では、Z値というものを求めて、そのZ値が基準値より大きいかどうかで、2つの対象に差があるのかを検定します。

今回のケースに合わせると、各数値は以下のとおりです。
n1=画像Aのクリック数
n2=画像Bのクリック数
r1=画像Aのコンバージョン数
r2=画像Bのコンバージョン数
p1=画像AのCVR
p2=画像BのCVR
H0：「画像Aと画像Bで、CVRに影響を与える差はない」
H1：「画像Aと画像Bで、CVRに影響を与える差がある」

検定統計式の分子に注目すると、2つのテストでのCVRの差の絶対値ですね。
よって、CVRの差が小さいほどZ0の値も小さくなります。
「画像Aと画像Bに差がない」という帰無仮説を考えると、Z0は限りなく0に近いはずで、
0から遠いほど、「めったに起こらない」＝帰無仮説は棄却できるということになります。

今回の件、実際にZ値を計算してみましょう。
n1=10000, n2=10000, r1=400, r2=340, p1=0.04, p2=0.034, p=0.037 を代入すると、

Z0≒2.25

Z値と言うのは、近似的に標準正規分布に従うとし
（本来、サンプルサイズの大きさに関わらず正確な検定結果を求めるには「フィッシャーの正確検定」が使われますが、
近似的に傾向を見るのであれば正規分布に従うとみて計算しても問題ないと思います）、
正規分布表によると、
Z=1.65のとき有意水準10%で有意 Z=1.65<2.25=Z0 より、有意差あり。
Z=1.96のとき有意水準5%で有意　Z=1.96<2.25=Z0 より、有意差あり。
Z=2.58のとき有意水準1%で有意　Z=2.58>2.25=Z0 より、有意差なし。

よって、
有意水準10%、5%のときは有意差ありなので帰無仮説は棄却＝ABテストの結果は、画像Aと画像Bの違いにより現れているとみなせる。
有意水準1%の時は、帰無仮説は棄却されない＝ABテストの結果は、画像Aと画像Bの違いによるとはみなせない（偶然の産物である）。

このように、有意水準を厳しくすればするほど当然結果も厳しくなりますので、
適切な有意水準を決めておくほうが良いですね。
よほど細かくABテストの分析をして改良しなければならない、という事情がない限りは、
有意水準は、10%、厳しくても5%、で十分ではないかと思います。

定期的にデータを基に計算を行い、有意差があるかを見ておけば、
有意差が出た時点で、テストとしては十分ということになります。
もしも、いつまでたっても有意差が出そうにもないならば、
テスト自体を見なおしたほうが良いかもしれません。
こうしてしっかりとロジックを基に判断したABテストを行うことで、
よりデータに沿って、ユーザーマインドを汲みとった改善が望めるのではないかと思います。

このように、しっかりと検定を行うと計算も煩雑であり、
なかなか日々行うには難しいという方が多いと思います。
（検定のロジックについては、なんとなくは知っておいたほうが良いと思いますが）

無料で検定をしてくれるサービスもあるようですが・・・わざわざ使いに別のサイトに行くのも面倒。
SiTest では、ABテストを行ったらその結果画面でそのまま検定を模した結果がご覧いただけます！

こちらが、SiTest でABテストを行った際の結果画面の下部を抜き出したものです。

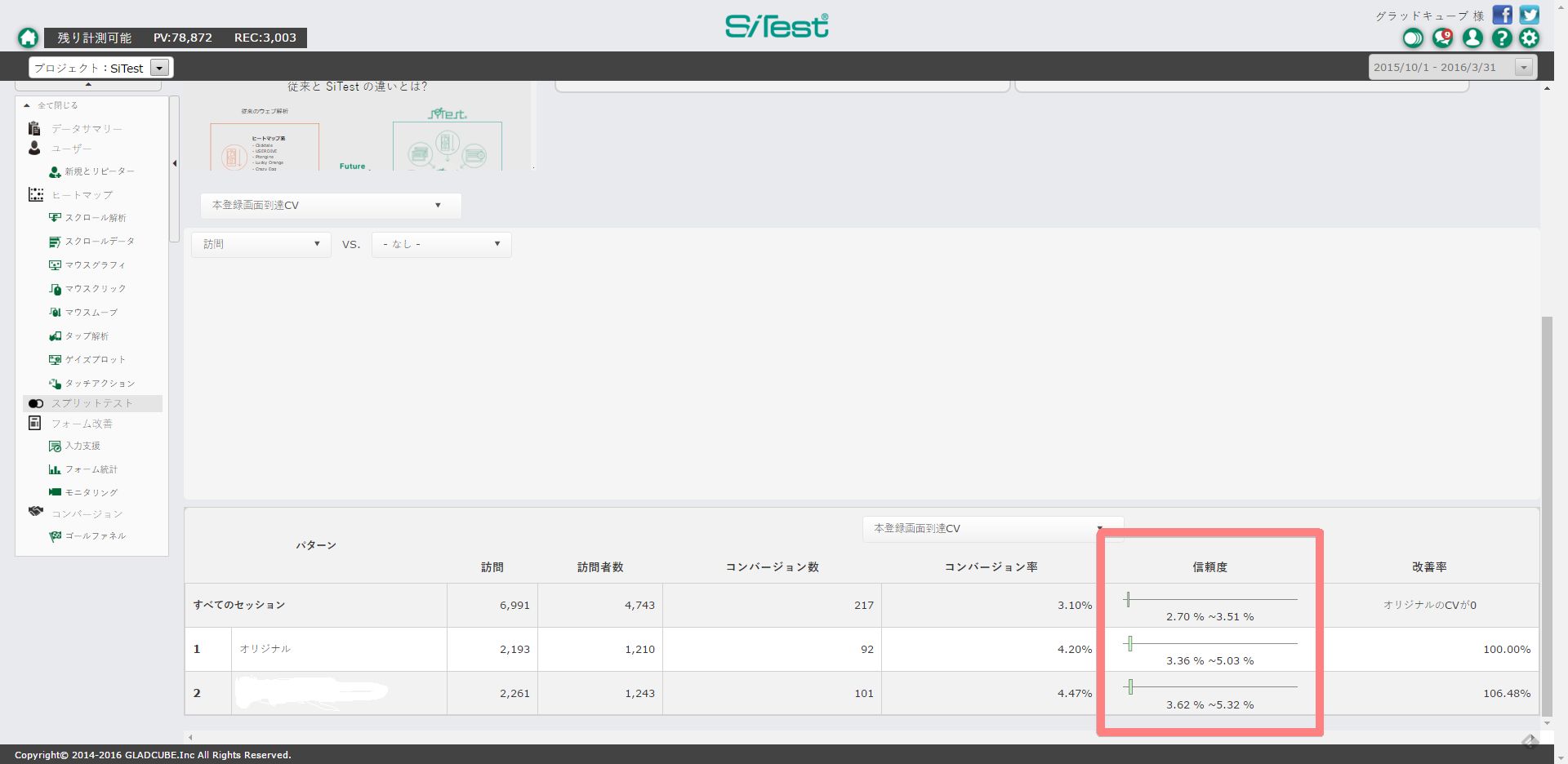
枠で囲った、「信頼区間」という項目をご覧下さい。
この「信頼区間」とは、CVRの数値にどれくらいのゆらぎが出るのかを表したものです。
95%の信頼区間（＝有意水準5%）で、この「信頼度」の数字は計算されています。
この「信頼区間」のそれぞれの域が被っていなければ、明らかにCVRが高い方がユーザーに受け入れられた方だと判断できます。

ぜひ、こちらもご覧いただけますと幸いです！

それでは、今回はこの辺りで失礼致します。
長々とお付き合いいただき、ありがとうございました。